Теорема про суму кутів трикутника. Чому дорівнює сума кутів опуклого багатокутника Теорема - чому рівні складені між собою кути довільного трикутника
Цілі і завдання:
Освітні:
- повторити та узагальнити знання про трикутник;
- довести теорему про суму кутів трикутника;
- практично переконатися у правильності формулювання теореми;
- навчитися застосовувати отримані знання під час вирішення завдань.
Розвиваючі:
- розвивати геометричне мислення, інтерес до предмета, пізнавальну та творчу діяльністьучнів, математичну мову, вміння самостійно здобувати знання.
Виховні:
- розвивати особисті якості учнів, таких як цілеспрямованість, наполегливість, акуратність, уміння працювати у колективі.
Обладнання:мультимедійний проектор, трикутники з кольорового паперу, УМК "Жива математика", комп'ютер, екран.
Підготовчий етап:вчитель дає завдання учневі підготувати історичну довідкупро теорему «Сума кутів трикутника»
Тип уроку: вивчення нового матеріалу
Хід уроку
I. Організаційний момент
Вітання. Психологічний настрій учнів працювати.
ІІ. Розминка
З геометричною фігурою "трикутник" ми познайомилися на попередніх уроках. Давайте повторимо, що нам відомо про трикутник?
Учні працюють у групах. Їм надано можливість спілкуватися один з одним, кожному самостійно будувати процес пізнання.
Що вийшло? Кожна група висловлює свої пропозиції, вчитель записує їх у дошці. Проводиться обговорення результатів:
Малюнок 1
ІІІ. Формулюємо завдання уроку
Отже, про трикутник ми знаємо вже досить багато. Але не все. У кожного з вас на парті є трикутники та транспортири. Як ви вважаєте, яке завдання ми можемо сформулювати?
Учні формулюють завдання уроку – знайти суму кутів трикутника.
IV. Пояснення нового матеріалу
Практична частина(Сприяє актуалізації знань та навичок самопізнання). Проведіть вимірювання кутів за допомогою транспортира та знайдіть їх суму. Результати запишіть у зошит (заслухати отримані відповіді). З'ясовуємо, що сума кутів у всіх вийшла різна (так може вийти, бо неточно доклали транспортир, недбало виконали підрахунок тощо).
Виконайте перегинання пунктирними лініями і дізнайтеся, чому ще дорівнює сума кутів трикутника:
а) 
Малюнок 2
б) 
Малюнок 3
в) 
Малюнок 4
г) 
Малюнок 5
д) 
Малюнок 6
Після виконання практичної роботи учні формулюють відповідь: Сума кутів трикутника дорівнює градусній мірі розгорнутого кута, тобто 180 °.
Вчитель: У математиці практична роботадає можливість лише зробити якесь твердження, та його треба довести. Твердження, справедливість якого встановлюється шляхом доказу, називається теоремою. Яку теорему ми можемо сформулювати та довести?
Учні: Сума кутів трикутника дорівнює 180 градусів.
Історична довідка:Властивість суми кутів трикутника було встановлено ще в Стародавньому Єгипті. Доказ, викладений у сучасних підручниках, міститься у коментарях Прокла до «Початків» Евкліда. Прокл стверджує, що цей доказ (рис. 8) було відкрито ще піфагорійцями (5 ст до н.е.). У першій книзі «Початок» Евклід викладає інший доказ теореми про суму кутів трикутника, який легко зрозуміти за допомогою креслення (рис. 7):

Малюнок 7

Малюнок 8
Креслення висвітлюються на екрані через проектор.
Вчитель пропонує за допомогою креслень довести теорему.
Потім доказ проводиться із застосуванням УМК «Жива математика». Вчитель на комп'ютері проектує доказ теореми.
Теорема про суму кутів трикутника: «Сума кутів трикутника дорівнює 180 °»

Малюнок 9
Доведення:
а) 
Малюнок 10
б) 
Малюнок 11
в) 
Малюнок 12
Учні зошита робить короткий запис докази теореми:
Теорема:Сума кутів трикутника дорівнює 180 °.

Малюнок 13
Дано:Δ АВС
Довести:А + В + С = 180 °.
Доведення:
Що потрібно було довести.
V. Фіз. хвилинка.
VI. Пояснення нового матеріалу (продовження)
Наслідок з теореми про суму кутів трикутника виводиться учнями самостійно, це сприяє розвитку вміння формулювати власну точку зору, висловлювати та аргументувати її:
У будь-якому трикутнику або всі кути гострі, або два гострі кути, а третій тупий або прямий.
Якщо трикутнику всі кути гострі, він називається гострокутним.
Якщо один із кутів трикутника тупий, то він називається тупокутним.
Якщо один із кутів трикутника прямий, то він називається прямокутним.
Теорема про суму кутів трикутника дозволяє класифікувати трикутники не тільки по сторонах, а й по кутах. (Під час введення видів трикутників учнями заповнюється таблиця)
Таблиця 1
| Вигляд трикутника | Рівностегновий | Рівносторонній | Різносторонній |
| Прямокутний | 
|

|
|
| Тупокутний | 
|

|
|
| Острокутний | 
|

|

|
VII. Закріплення дослідженого матеріалу.
- Розв'язати задачі усно:
(Креслення висвітлюються на екрані через проектор)
Сума внутрішніх кутів трикутника дорівнює 180 0 . Це одна з основних аксіом геометрії Евкліда. Саме цю геометрію вивчають школярі. Геометрію визначають наукою, що вивчає просторові форми справжнього світу.
Що спонукало давніх греків розробити геометрію? Потреба вимірювати поля, луки – ділянки земної поверхні. У цьому древні греки прийняли, що Землі горизонтальна, плоска. З урахуванням цього припущення і створювалися аксіоми Евкліда, у тому числі і про суму внутрішніх кутів трикутника 180 0 .
Під аксіомою розуміється становище, яке вимагає докази. Як це треба розуміти? Висловлюється побажання, яке влаштовує людину, і далі воно підтверджується ілюстраціями. Але все, що не доведено – вигадка, те, чого немає насправді.
Приймаючи земну поверхню горизонтальної, давні греки автоматично набули форми Землі плоскої, але вона інша – сферична. Горизонтальних площин та прямих ліній у природі взагалі немає, бо гравітація викривляє простір. Прямі лінії та горизонтальні площини є лише у мозку голови людини.
Тому геометрія Евкліда, яка пояснює просторові форми вигаданого світу, є симулякром - копією, що не має оригіналу.
Одна з аксіом Евкліда свідчить, що сума внутрішніх кутів трикутника дорівнює 1800. Насправді у реальному викривленому просторі, чи сферичної поверхні Землі, сума внутрішніх кутів трикутника завжди більше 180 0 .
Розмірковуємо так. Будь-який меридіан на глобусі перетинається з екватором під кутом 90°. Щоб отримати трикутник, потрібно від меридіана відсунути інший меридіан. Сума кутів трикутника між меридіанами та стороною екватора становитиме 180 0 . Але ще залишиться кут біля полюса. У результаті сума всіх кутів і становитиме понад 180 0 .
Якщо на полюсі сторони перетнуться під кутом 90 0 то сума внутрішніх кутів такого трикутника буде 270 0 . Два меридіани, що перетинаються з екватором під прямим кутом у цьому трикутнику, будуть паралельними один одному, а на полюсі, що перетинаються один з одним під кутом 90 0 стануть перпендикулярами. Виходить, дві паралельні лінії на одній площині не тільки перетинаються, але можу бути перпендикулярами на полюсі.
Звичайно, сторони такого трикутника будуть не прямими лініями, а опуклими, що повторюють сферичну форму земної кулі. Але саме такий реальний світ простору.
Геометрію реального простору з урахуванням його кривизни у середині ХІХ ст. розробив німецький математик Б. Ріман (1820–1866). Але про це школярам не кажуть.
Отже, евклідова геометрія, що набуває форми Землі плоскої з горизонтальною поверхнею, чого насправді немає, є симулякрою. Ноотик – геометрія Рімана, що враховує кривизну простору. Сума внутрішніх кутів трикутника в ній більша за 180 0 .
Трикутник . Гострокутний, тупокутний та прямокутний трикутник.
Катети та гіпотенуза. Рівностегновий та рівносторонній трикутник.
Сума кутів трикутника.
Зовнішній кут трикутника. Ознаки рівності трикутників.
Чудові лінії та точки у трикутнику: висоти, медіани,
бісектриси,серединні e перпендикуляри, ортоцентр,
центр тяжкості, центр кола, центр вписаного кола.
Теорема Піфагора. Співвідношення сторін у довільному трикутнику.
Трикутник – це багатокутник із трьома сторонами (або трьома кутами). Сторони трикутника часто позначаються малими літерами, які відповідають великим літерам, що позначають протилежні вершини.
Якщо всі три кути гострі (рис.20), то це гострокутний трикутник
. Якщо один із кутів прямий(C, рис.21), то це прямокутний трикутник; сторониa, b, що утворюють прямий кут, називаються катетами; сторонаc, протилежна прямому куту, називається гіпотенузою. Якщо один ізкутів тупий (B, рис.22), то це тупокутний трикутник.
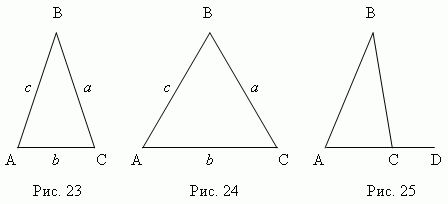
Трикутник ABC (рис.23) - рівнобедрений, якщо двійого сторони рівні (a=
c); ці рівні сторони називаються бічними, третя сторона називається основоютрикутник. Трикутник ABC (рис.24) - рівносторонній,
якщо Усейого сторони рівні (a
=
b
=
c). У загальному випадку ( a ≠ b ≠ c)
маємо нерівностороннійтрикутник .
Основні властивості трикутників. У будь-якому трикутнику:
1. Проти більшої сторони лежить більший кут, і навпаки.
2. Проти рівних сторін лежать рівні кути, і навпаки.
Зокрема, всі кути в рівностороннімтрикутнику рівні.
3. Сума кутів трикутника дорівнює 180 º .
З двох останніх властивостей випливає, що кожен кут у рівносторонньому
трикутнику дорівнює 60 º.
4. Продовжуючи одну із сторін трикутника (AC, рис.25), отримуємо зовнішній
кут BCD . Зовнішній кут трикутника дорівнює сумі внутрішніх кутів,
не суміжних з ним : BCD = A + B.
5. Будь-яка сторона трикутника менша від суми двох інших сторін і більше
їх різниці (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).
Ознаки рівності трикутників.
Трикутники рівні, якщо вони відповідно рівні:
a ) дві сторони та кут між ними;
b ) два кути і прилегла до них сторона;
c) три сторони.
Ознаки рівності прямокутних трикутників.
Два прямокутнихтрикутника рівні, якщо виконується одна з наступних умов:
1) рівні їх катети;
2) катет та гіпотенуза одного трикутника рівні катету та гіпотенузі іншого;
3) гіпотенуза та гострий кут одного трикутника рівні гіпотенузі та гострому куту іншого;
4) катет і прилеглий гострий кут одного трикутника дорівнюють катету та прилеглому гострому куту іншого;
5) катет і протилежний гострий кут одного трикутника дорівнюють катету і протилежному гострому кутку іншого.
Чудові лінії та точки у трикутнику.
Висота трикутника - цеперпендикуляр,опущений з будь-якої вершини на протилежний бік ( або її продовження). Ця сторона називаєтьсяосновою трикутника . Три висоти трикутника завжди перетинаютьсяв одній точцізваної ортоцентромтрикутник. Ортоцентр гострокутного трикутника (точка O , рис.26) розташований усередині трикутника, аортоцентр тупокутного трикутника (точка O , Мал.27) – зовні; Ортоцентр прямокутного трикутника збігається з вершиною прямого кута.
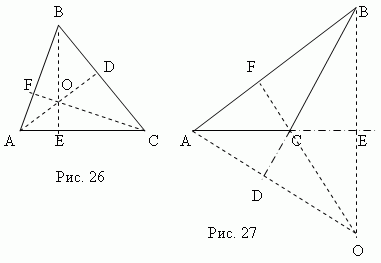
Медіана – це відрізок , що з'єднує будь-яку вершину трикутника із серединою протилежної сторони. Три медіани трикутника (AD, BE, CF, рис.28) перетинаються в одній точці O завжди лежить всередині трикутникаі є його центром важкості. Ця точка ділить кожну медіану щодо 2:1, рахуючи від вершини.
Бісектриса – це відрізок бісектрисикута від вершини до точки перетину з протилежною стороною. Три бісектриси трикутника (AD, BE, CF, рис.29) перетинаються в одній точці О, що завжди лежить усередині трикутникаі що є центром вписаного кола(Див. розділ «Вписаніта описані багатокутники»).
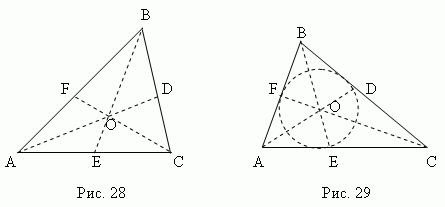
Бісектриса ділить протилежний бік на частини, пропорційні прилеглим сторонам ; наприклад, на рис.29 AE: CE = AB: BC.
Середній перпендикуляр – це перпендикуляр, проведений із середньоїточки відрізка (сторони). Три серединні перпендикуляри трикутника АВС(KO, MO, NO, рис.30 ) перетинаються в одній точці О, що є центром описаного кола (точки K, M, N – середини сторін трикутника ABC).
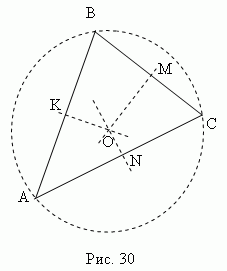
У гострокутному трикутнику ця точка лежить усередині трикутника; у тупокутному – зовні; у прямокутному - у середині гіпотенузи. Ортоцентр, центр тяжкості, центр описаного та центр вписаного кола збігаються лише у рівносторонньому трикутнику.
Теорема Піфагора. У прямокутному трикутнику квадрат довжинигіпотенузи дорівнює сумі квадратів довжин катетів.
Доказ теореми Піфагора очевидно випливає з рис.31. Розглянемо прямокутний трикутник ABC з катетами a, bта гіпотенузою c.

Збудуємо квадрат AKMB , використовуючи гіпотенузу AB як бік. Потімпродовжимо сторони прямокутного трикутника ABC так, щоб отримати квадрат CDEF сторона якого дорівнюєa + b.Тепер ясно, що площа квадрата CDEF дорівнює ( a + b) 2 . З іншого боку, ця площа дорівнює суміплощ чотирьох прямокутних трикутниківі квадрата AKMB, тобто
c 2 + 4 (ab / 2) = c 2 + 2 ab,
звідси,
c 2 + 2 ab= (a + b) 2 ,
і остаточно маємо:
c 2 =a 2 + b 2 .
Співвідношення сторін у довільному трикутнику.
У загальному випадку (для довільного трикутника) маємо:
c 2 =a 2 + b 2 – 2ab· cos C,
де C – кут між сторонамиaі b .
Доведення
Нехай ABC" - Довільний трикутник. Проведемо через вершину B пряму, паралельну до прямої AC (така пряма називається прямою Евкліда). Зазначимо на ній крапку D так, щоб точки A і D лежали по різні боки від прямої BC. Кути DBCі ACBрівні як внутрішні навхрест лежачі, утворені січучою BCз паралельними прямими ACі BD. Тому сума кутів трикутника при вершинах Bі Здорівнює куту ABD.Сума всіх трьох кутів трикутника дорівнює сумі кутів. ABDі BAC. Так як ці кути внутрішні односторонні для паралельних ACі BDпри січній AB, їх сума дорівнює 180°. Теорему доведено.
Наслідки
З теореми випливає, що у будь-якого трикутника два кути гострі. Справді, застосовуючи доказ протилежного , припустимо, що з трикутника лише одне гострий кут чи взагалі немає гострих кутів. Тоді цей трикутник має принаймні два кути, кожен з яких не менше 90°. Сума цих кутів не менша за 180°. І це неможливо, оскільки сума всіх кутів трикутника дорівнює 180°. Що й потрібно було довести.
Узагальнення у симплекс теорії
Де -кут між i і j гранями симплексу.
Примітки
- На сфері сума кутів трикутника завжди перевищує 180°, різниця називається сферичним надлишком та пропорційна площі трикутника.
- У площині Лобачевського сума кутів трикутника завжди менша за 180°. Різниця також пропорційна площі трикутника.
Див. також
Wikimedia Foundation. 2010 .
Дивитись що таке "Теорема про суму кутів трикутника" в інших словниках:
Властивість багатокутників у евклідовій геометрії: Сума кутів n кутника дорівнює 180 ° (n 2). Зміст 1 Доказ 2 Примітка … Вікіпедія
Теорема Піфагора одна з основних теорем евклідової геометрії, що встановлює співвідношення між сторонами прямокутного трикутника. Зміст 1 … Вікіпедія
Теорема Піфагора одна з основних теорем евклідової геометрії, що встановлює співвідношення між сторонами прямокутного трикутника. 1 Формулювання 2 Докази … Вікіпедія
Теорема косінусів узагальнення теореми Піфагора. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними. Для плоского трикутника зі сторонами a, b, cта кутом α… … Вікіпедія
Цей термін має й інші значення, див. Трикутник (значення). Трикутник (в евклідовому просторі) це геометрична фігура, утворена трьома відрізками, які з'єднують три не лежать на одній прямій точці. Три точки, … … Вікіпедія
Стандартні позначення Трикутник найпростіший багатокутник, що має 3 вершини (кута) та 3 сторони; частина площини, обмежена трьома точками, що не лежать на одній прямій, і трьома відрізками, що попарно з'єднують ці точки. Вершини трикутника … Вікіпедія
Давньогрецький математик. Працював у Олександрії III в. до зв. е. Головна праця «Початку» (15 книг), що містить основи античної математики елементарної геометрії, теорії чисел, загальної теорії відносин та методу визначення площ та обсягів, … Енциклопедичний словник
- (Помер між 275 і 270 до н. е.) давньогрецький математик. Відомості про час і місце його народження до нас не дійшли, проте відомо, що Евклід жив в Олександрії і розквіт його діяльності припадає на час царювання в Єгипті Птолемея I. Великий Енциклопедичний словник
Геометрія, подібна до геометрії Евкліда в тому, що в ній визначено рух фігур, але відрізняється від евклідової геометрії тим, що один з п'яти її постулатів (другий або п'ятий) замінений його запереченням. Заперечення одного з евклідових постулатів. Енциклопедія Кольєра
Сума кутів трикутника- важлива, але досить проста тема, що проходять у 7 класі на геометрії. Тема складається з теореми, короткого доказу та кількох логічних наслідків. Знання цієї теми допомагає у вирішенні геометричних завданьпри подальшому вивченні предмета.
Теорема – чому рівні складені між собою кути довільного трикутника?
Теорема говорить - якщо взяти будь-який трикутник незалежно від його виду, сума всіх кутів незмінно становитиме 180 градусів. Доводиться це так:
- для прикладу беруть трикутник АВС, через розташовану на вершині точку проводять пряму лінію і позначають її, як «а», пряма «а» при цьому строго паралельна стороні АС;
- між прямою «а» і сторонами АВ і ПС позначають кути, маркуючи їх цифрами 1 і 2;
- кут 1 визнають рівним куту А, а кут 2 - рівним куту С, оскільки ці кути вважаються навхрест лежачими;
- таким чином, сума між кутами 1, 2 і 3 (який позначається на місці кута) визнається рівною розгорнутому куту з вершиною - і становить 180 градусів.
Якщо сума кутів, позначених цифрами, становить 180 градусів, то сума кутів А, В і С визнається рівною 180 градусам. Це правило правильне для будь-якого трикутника.
Що випливає з геометричної теореми
Прийнято виділяти кілька наслідків із наведеної теореми.
- Якщо в задачі розглядається трикутник з прямим кутом, то один з його кутів буде за замовчуванням 90 градусів, а сума гострих кутів також становитиме 90 градусів.
- Якщо йдеться про прямокутний рівнобедрений трикутник, то його гострі кути, що в сумі складають 90 градусів, окремо дорівнюватимуть 45 градусам.
- Рівносторонній трикутник складається з трьох рівних кутів, відповідно, кожен з них дорівнюватиме 60 градусам, а в сумі вони становитимуть 180 градусів.
- Зовнішній кут будь-якого трикутника дорівнюватиме сумі між двома внутрішніми кутами, що не прилягають до нього.
Можна вивести наступне правило - у будь-якому з трикутників є як мінімум два гострі кути. У деяких випадках трикутник складається із трьох гострих кутів, а якщо їх тільки два, то третій кут буде тупим або прямим.


